A novel AI-acceleration paper presents a method to optimize sparse matrix multiplication for machine learning models, particularly focusing on structured sparsity. Structured sparsity involves a predefined pattern of zero values in the matrix, unlike unstructured sparsity where zeros can occur anywhere. The research was conducted by Democritus University of Thrace (DUTH) in Greece and was sponsored by Codasip University Program.
Structured sparsity has emerged as a promising approach to streamline the complexity of modern Machine Learning (ML) applications and facilitate the handling of sparse data in hardware. Accelerating ML models, whether for training or inference, heavily relies on efficient execution of equivalent matrix multiplications, which are often performed on vector processors or custom matrix engines.
Integrating structured sparsity into existing vector execution
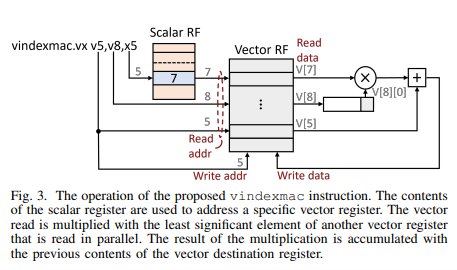
The aim of this study was to integrate the simplicity of structured sparsity into existing vector execution flow and vector processing units (VPUs), thus expediting the corresponding matrix multiplications with minimal redesign in mind. To achieve this goal, a novel vector index-multiply-accumulate instruction is introduced. This instruction facilitates low-cost indirect reads from the vector register file, thereby reducing unnecessary memory traffic and enhancing data locality.
Key points of their approach include:
- Vectorized sparse matrix multiplication: DUTH adapted a vectorized row-based matrix multiplication algorithm to handle structured sparse data. This involved loading only the nonzero elements and their column indexes from one sparse matrix and selecting corresponding rows from the other matrix for multiplication.
- Introduction of a new instruction: They introduced a new vector instruction called vindexmac (vector index-multiply-accumulate) to optimize the computation from point 1. This instruction allows for low-cost indirect reads from the vector register file, reducing unnecessary memory traffic and instruction overhead.
- Hardware implementation: The proposed vector instruction is integrated into a high-end decoupled RISC-V vector processor at minimal hardware cost. Evaluation using Gem5 simulation demonstrated significant speedups when executing Convolutional Neural Networks (CNNs) pruned for structured sparsity.
- Optimization for local data usage: The researchers preloaded tiles of one of the matrices into the vector register file to improve data locality and reduce memory traffic during computation. This optimization exploits the regular structure of the sparse matrix A to determine which rows of B need to be preloaded.
DUTH’s approach to implementing vectorized matrix multiplications with sparse data
There are various approaches to implementing vectorized matrix multiplications with sparse data. One particularly effective method is the row-wise approach, also referred to as Gustavson’s algorithm, which has demonstrated high efficiency in calculating the matrix product A × B. The product of the matrix multiplication is produced row-wise, as follows:
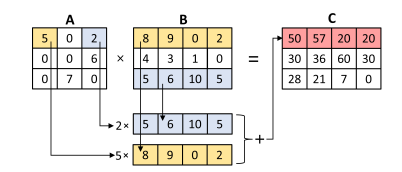
You vector-load the first row of A, and then load all rows of B. Each row of B is multiplied with one of the elements of the loaded row of A. The results are accumulated row-wise in C. To avoid multiplying the zero elements the following algorithm can be used with which you only load the rows of B that correspond to non-zero columns of A:

The structured-sparse format of matrix A helps in eliminating unnecessary multiplications in sparse-dense multiplication. However, a critical bottleneck arises from the still relatively frequent vector loads from memory for the rows of matrix B, as indicated in lines 8 and 9 of Algorithm 2. To address this challenge, we can exploit the structured sparsity of matrix A to minimize memory traffic and enable computations to utilize local data already present in the vector register file.

The vindexmac instruction streamlines the process by replacing the three instructions, including a vector load from memory, from lines 8 to 10 of Algorithm 2. Consequently, the need for vector loading from memory is eliminated with the caveat of needing to preload a tile of matrix B. Furthermore, the vindexmac instruction efficiently computes a vector containing partial results corresponding to a row of the result matrix C.
Since B is preloaded and accessing it is done through the vector register file reads, we can see in Algorithm 3 that the number of times B rows are loaded is now outside of the inner for-loop, meaning much less loads overall. As the number of zero elements of both A and B is known beforehand and is done in a very structured manner, it means this preloading and implementing the new instruction can be done very efficiently.
Conclusion: substantial speedups
This is just a very brief and high-level overview of the technical details and more can be inferred from the actual paper.
The newly proposed instruction has been seamlessly integrated into a decoupled RISC-V vector processor with minimal hardware overhead. Extensive evaluations have showcased substantial speedups ranging from 1.80× to 2.14× compared to state-of-the-art vectorized kernels. These improvements are particularly pronounced when executing layers with varying degrees of sparsity sourced from cutting-edge Convolutional Neural Networks (CNNs).
Additionally, optimizations regarding the sparse data placement, across the scalar and vector register files, are planned for future work.
Soon, this new instruction will be integrated into a VPU extended Codasip L31 core using Codasip Studio, further enhancing the capabilities of the vector processor for sparse matrix multiplication tasks.
The collaboration between DUTH University and Codasip’s University showcases how industry tools and sponsorship can help drive academic research and development of novel and state-of-the-art solutions in processor and system design for AI inference acceleration and in turn how new ideas can be integrated into existing industry products.
